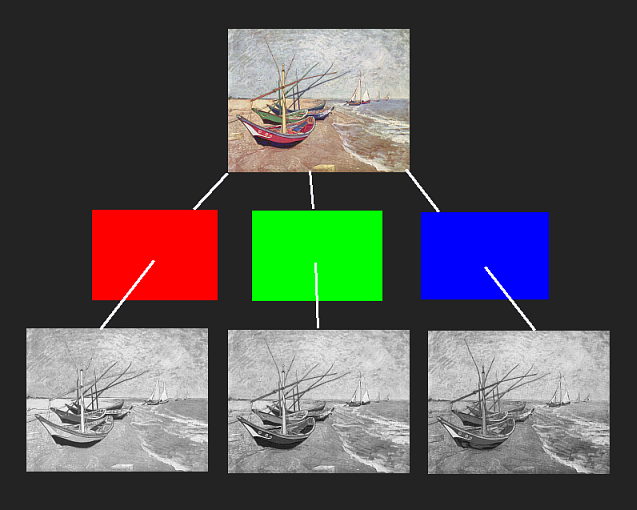
I should like to bring up the by now classical experiment on colour vision by Edwin H. Land, published in 1959. He was using two photographic black-and-white transparencies representing one and the same coloured scene. One of them was taken through a red filter, the other one through a blue-green filter.
Land observed that when he projected the two pictures onto each other, the first one through the red filter and the second one without any filter – in other words by the unmodified light flux from the lamp of the projector – the resulting image on the screen showed a diversity of colours; not only the various shades of pink one would expect from the ordinary laws of additive colour mixing. In one of the first papers, where he presents his finding, Land begins with the bold statement:
"We have come to the conclusion that the classical laws of color mixing conceal great basic laws of color vision".
How could he claim that? Let us take a look at the experiment in closer detail. You may be familiar with the method of colour reproduction by help of so called "colour separation". The subject is photographed through a red, a green and a blue filter and when the three b/w photos (after being turned into diapositives) are projected onto each other, through their respective colour filter, the colours of the objects of the original scene are recreated.

So, in principle, we first analyse the motive by a subtractive method, using three colour filters, and then synthesise a reproduction of it by an additive method, superimposing colored lights.
This method of colour photography was invented already by James Clerk Maxwell in 1861. He was also the one who quantitatively investigated the so called trichromaticity of human colour vision, which is the scientific basis for this kind of colour reproduction. In principle his method of colour reproduction is still used today on our computer screens and mobile phones, as well as digital projectors.
Now Land claimed that it if keep the red, but skip the blue record and project the green record without a colour filter – in other words in "white light" – you still get almost the whole gamut of colour. From the laws of additive colour mixing (i.e. when superimposing coloured lights) you would naively expect only various shades of rose, something like this:
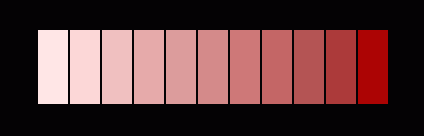
So how could one possibly get a variety of hues in the projected image? Let us look a bit futher into the issue!
As I just said, even modern digital photography builds on the Maxwell colour separation method. However the information about the distribution of light intensity over the picture area – as detected through a red, a green and a blue filter – is not stored as shades on a photographic film but in numerical form. The data prescribe how each minute area in the picture, defined as a "pixel", should be assigned a colour, specified by a triple of numbers (r,g,b). These numbers govern the excitation of the Red, Green and Blue sub-pixels on the screen where the image is to be presented.
Here is a digital reproduction of a postcard picture. Using this I will try to make a digital simulation of the process of additively mixing a red and a neutral aspect of the original.

Usually we think about the screen image point-wise, that is as a fine-graded chequered pattern of pixels, each one with its (r,g,b) triple. This triple indicates the colour at that point. This is a misleading view on the matter, according to Edwin Land. Alternatively, and better for our purpose, is to regard it as three essentially independent superimposed images: a red one, a green one and a blue one. (As it was done photographically.) The tree images may be displayed separately and look like this:

In order to simulate the Land experiment, we cannot manipulate the built-in colour filters, but we can manipulate the digital information. First step is to expand the green record to embrace all three channels. Which means that the green record will appear on the screen as an image in black and white. In other words: as projected without a green filter!
Next step is to simulate the optical superposition of the red and the neutral images, by adding the red record to the R-channel. In doing this one can test various proportions, to search for an optimal mixture.

The two images, we want to add, have to share the luminance available on the screen. Let us say, we begin with the neutral record at maximum luminance level. We then add the red record, sucessively increasing its intensity while simultaneously decreasing the intensity of the neutral image, until the palette transformation ends up with pure red at max screen luminance. (This is shown as a 30 seconds process on the video.)
In summary, the transformation of the original palettte (r,g,b) into the new palette (r',g',b') is given by
Let me show you an example of how it can look. A proportion of 40% neutral and 60% red gave this striking result. The wide range of proportions within which you get essentially the same hues at the same objects is however a remarkable fact, indicating that the observed object colours are invariant under change of relative redness of the total scene.

So what do we see here? An astonishing multitude of various hues – or only nuances of red together with grey and black?
Personally I see a lot of colours: the red boat in the foreground, with its yellow mast, brown yard and a dark blue seat, box, or whatever it is, lying inside; furthermore the side of the second boat is green. The sea and sky are of course, as expected, here and there slightly blueish. The more I look into the picture – letting my gaze freely move around, exploring it – the more these colours establish themselves as undisputable.
Maybe you suspect that I see all these hues only because I am acquainted with the original picture? Well, if so, what is the difference between seeing a colour and imagine that one sees a colour?
Observe however the following distinction. I am not asking what colours you see on various spots on the screen. I am asking what colours you see in the picture, displayed on the screen. This is a huge difference.
Perception psychologist James J Gibson says:
What is a picture? A picture is a surface that specifies something other than what it is. (...) The picture is both a scene and a surface, and the scene is paradoxically behind the surface.
Hence, I do not see the colours of the pixels on the surface of the screen, but spontaneously look into the scene behind the screen, where I get a view on a shore with a row of colourfully painted boats, all in reddish light.
It is also a question of perceptual attitude. If I focus on the blue box in the nearest boat, to my disappointment I find: it is dark grey. But if I let the picture just be there, without scrutinizing it, taking it in as a whole .. there it is, colourful again, including that enigmatic blue box in the red boat.
Whether or not this is a true reproduction of the original postcard picture is unimportant. The point with Edwin Land's demonstration is simply that it shows that a sufficiently complicated picture, based on at least two different chromatic aspects of the scene, tends to create its own "colour universe". According to which "great basic laws of color vision" remains to be found out.
For those of you, who are familiar with the colorimetric system, it might be informative to see a plot of the points of the palette in a CIE chromaticity diagram. We see that in case of the two-colour version the chromaticities of the points, constituting the screen-image, follow a straight line between the red primary of the RGB triangle and the white point. Compare this with the spread out of chromaticities for the full three-channel digital reproduction of the postcard picture! The corresponding palette mosaics vividly illustrate the difference.
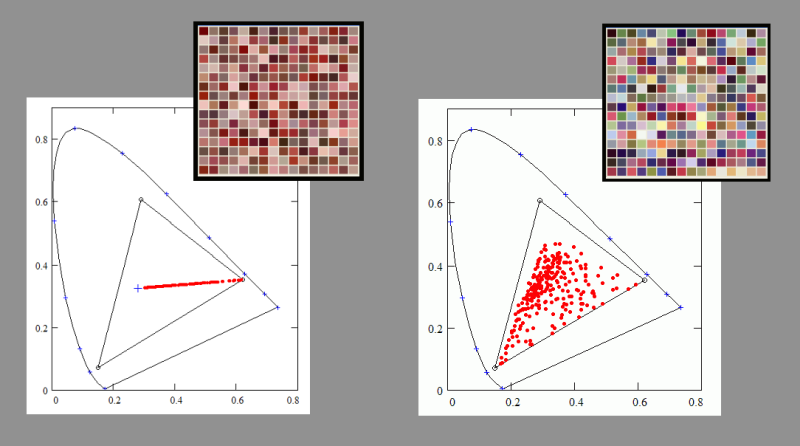
CIE 1931 chromaticity diagrams together with JASC-palettes
The CIE-diagram shows that all colours in the two-colour-projection version of the boat picture have one and the same so called "dominant wavelength", at about 610 nm. Despite this they can appear with any hue of the spectrum. This was probably what Edwin Land meant when critizising "the classical laws of color mixing". In a sufficiently complex picture (a "natural image") the hue qualities are not determined by the chromaticity of the light locally detected at the retina. Which is to say that the celebrated colour sequence of the newtonian spectrum has poor explanatory value when we are dealing with the colours seen in a pictorial representation.
If you are not familiar with the formal concepts of colorimetry a closer look at the palette-issue may be helpful, to underline what I pointed out above.
The digital image has been scanned with the aim of selecting 256 specific (r,g,b) triples making up the image, ready to be further analysed and presented on a screen. The resulting so-called JASC-palette is a 256 x 3 matrix. In other words a long series of (r,g,b)-triples. In order to visualise this long "worm", it has been folded into a 16 x 16 arrangement. This is already a kind of pictorial illustration of the palette and looks more vivid and colourful than what it is intended to illustrate.
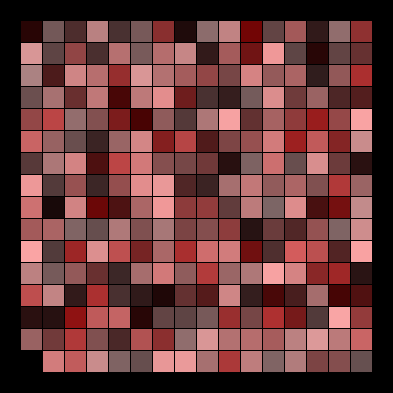
Exactly the same palette (sic!), systematically ordered after increasing r-values and on each row ordered after increasing g-values, looks as follows. More informative, but less spectacular, no doubt.
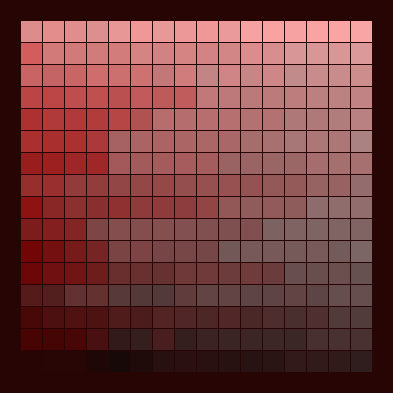
However this, as well as the foregoing, are representations of a specific palette for a specific picture. Namely the boat-picture above.
A general palette, valid for any two-image projection of the type (r,0,0)+(g,g,g), can be constructed in the following way. We start with two colour scales. A grey-scale, running from left to right, together with a red-scale, running upwards, like this:

Superimposing them optically gives us a palette with 256 individual colours. Here with 60% red and 40% neutral:
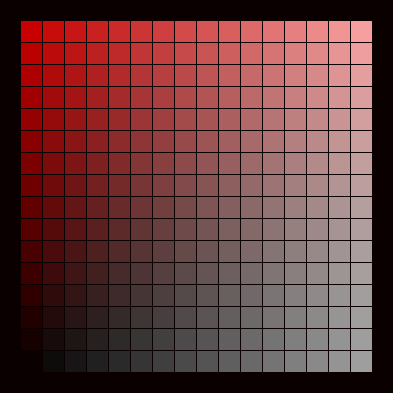
These are all possible variations. This palette contains no other hues than a certain red. Observe that it is from this palette that all colours appearing in the boat-picture are fetched. Locally, on the screen there are no other colours. This is remarkable!
It must have been this observation that fascinated and puzzled Edwin Land and made him state that the simple rules of additive colour mixing cannot explain the multiplicity of hues you see in the displayed picture.
Evidently it is the figurative distribution of the palette-colours over the picture area – the pattern on the screen – that determines the various hues you see in any picture of the red+white-projection type. I will show you an example of this.
Let us try the following. Select 36 of the colours in the palette above! Here they are, each with its particular chromaticity and lightness. Again nothing particularly remarkable.

But now fill in the interspace between the individual patches. This makes the picture into a whole, whithin which the individual patches get their roles. A multitude of hues appear, vaguely but irresistibly manifesting themselves, as you wander around in the picture with your gaze. (Take your time!)

This striking demonstration was presented in a paper dealing with Land´s experiment by Michael Wilson and Ralph Brocklebank. It is remarkable that it is at the dark values that the conspicous colours tend to appear.
As with all pictures it lies near at hand to se it "as" something. For instance seeing it as a number of colour samples on a common light grey background and the whole illuminated with reddish light. What binds the colour patches together is the common backgrund and the common illumination.
What could be the explanation of the appearance of blue and green on certain objects in the boat-picture? Let us compare the two records, the one taken through red filter and the one through green.

In practical life, what characterises a blue surface is that it does not reflect radiation of long and medium wavelenghts, within the visible range. It is this selective darkening that defines the blue colour.
In consequence of this the blue object is almost totally without any red contribution. (See the left picture, where it is dark grey, almost black.) This informs the perceptual system that the object might be blue, green, blue-green or neutral darkgrey. But there is no information as to which of these alternatives is to be chosen. This information is normally supplied by the blue record, which in our case has been deliberately suppressed by setting it equal to the green record.
So why do I spontaneously see the box as blue and the boat-side as green? This still remains enigmatic. From the point of view of hue information the picture is ambiguous. It can be seen in several ways.
A further important feature of the phenomenon is that the box in the boat looks blue independently of the proportion red/white in the mixture. (See the video, illustrating this article.) In fact, the pixels constituting the box look like this during the process of changing mixture. Nota bene, if taken out of its "natural" context.

The local colour stimulus changes, according to the amount of red, but one and the same dark blue is seen, as an invariant object colour under continuosly changing illumination. This is the magic of the Land demonstration. The colours of objects are there or are not -- we may feel unsafe about it -- because here a "higher" law of colour-vision is activated, namely the possibility to recognize object colours "through" a coloured illumination, judged from the overall look of the image.
The said is true for a "natural image", in the sense that the lightness pattern plays a decisive role. For an arbitrary picture this need not necessarily be true. (But see the Wilson-Brocklebank demonstration above!)
Observe that projecting the green-channel record with neutral light is not the same thing as having neutral light as illumination of the objects in the scene represented. The neutral green-projection (g,g,g) gives strong (but probably false!) information that all objects in the scene are painted in white-grey-black. However the addition of the red-projection (r,0,0) confuses this information, because it signals that there are red, orange and brown objects and then probably blue, green and bluegreen objects as well. Namely where the red record is dark. Leading to unsaturated reds.
From what is said above one understands that the differences in gradation between the red and the green record is essential for the phenomenon we are discussing. It is not only a question of mixing red and white light. For instance, if we use identically the same record for the red and the neutral image, then there will be no hues other than the expected rosy ones. The excess of red is evidently not the decisive factor. Here all points have one and the same saturation and that is evidently not enough variation for colour to enter the scene.

All three channels with the red record (left) or the green record (right).
That is (r,0,0)+(r,r,r) and (g,0,0)+(g,g,g) respectively.
To observe or register the scene with its objects in at least two different lights (for instance, as in our case, by using a red and a green filter in front of the camera lens) seems to be a necessary condition for the appearance of a variety of hues.
Fact is that the two objects, observed at sufficiently close range, even for me, are just grey; the boatside slightly lighter than the box in the red boat.

Is it this small difference in lightness that counts, when the neutral point is split up in two directions: one towards green, the other one towards blue? The darkest one gets the role of blue, the brigher one becomes green.
Let us test this hypothesis. We can make both of them equally dark, or equally light, or we can interchange the colours: making the boat-side dark and the seat light.

So how do they look? Is the darker one always blue and the lighter one green? Well, to me -- at first moment at least -- the one where both objects are dark have the most prominent colours: dark blue and dark green. The lighter green of the original (upper left) looks more in the direction of cyan.
Even more. In the reversed case (light box, dark boat) I see the box as light-grey (or maybe even light-blue) and the boat-side dark-green. So the idea that the darkest area always takes on a blue hue, doesn't seem to hold.
However, the seat is surrounded with brown and red colours, so there might be a contrast effect involved. The boat-side is not embedded in warm colours, so it does not invite blue, even when it has low lighness.
To be sure, the two-colour projection demonstrations can be varied infinitely. One can test with a warmer red, or a cooler red. One may try with other registrations than the green one for the neutral image. And, of course, one may repeat the experiment with any other digital picture of a scene with coloured objects.
Furthermore it is of course tempting to play around with two-colour mixing in a more general sense, not limited to red+white. For instance, to study complementary colour pairs, such as red+cyan: (r,0,0)+(0,g,g). Even in this case all colours have chromaticities along a straight line from the red primary of the RGB triangle through the white point, but streching out on the opposite side of this, which means definite cyan colours. Hence one can chose the mixing ratio such as to avoid the overall red tone and get a picture in neutral light, consequently more similar to the original. Perceptually this is however something different. In a sense white, black and grey are not "colours". And white light is not just a kind of light among lights of diverse colours.
Instead of bringing up these intriguing aspects on our topic, let me put an end here and finish with a few remarks concerning what we have learnt.
You may raise the objection to all this: "What is the idea of playing around with two-colour mixing, when the well established three-colour procedure gives much more convincing colour reproduction?"
We are deliberately using a well-established technical reproduction method in a wrong, not intended way. To skip the green filter and leave out the blue record in recreating the colours seems nonsensical. But sometimes a mistake can lead to a new insight.
When Goethe looked through a glass prism towards a white wall he expected to see a multitude of colours. But there where none. In his disappointment he concluded that Newton's theory was wrong. But he was mistaken. He had no reason, from newtonian theory, to expect colours to appear under these conditions. His inadequate way of using the prism to produce colours had however directed his attention to something that Newton had overlooked – namely that colour belongs to images. And images are built on contrasts, mainly in terms of bright and dark. Newton had ignored the role of darkness. Darkness is always, in some way or other, together with light a condition for the appearance of colour.
Our case is similar. Edwin Land's demonstration convincingly shows that the classical (or perhaps rather "Newtonian") psycho-physical theory of colour vision is inadequate. The hues are not determined by the chromaticity of the light, that is, they are not directly related to the series of hues of the spectrum, as Newton had proposed. Rather, it seems to be the pattern of lightness and saturation over the image that supplies the decisive information to the visual system. Namely in the following way, acccording to Land's "retinex theory" (as I have understood it).
In a way we actually have three different eyes in one, namely corresponding to the three types of cones in the retina – being sensitive essentially in the short-, middle- and long-wave regions of the visible interval of radiation. Let us assume that each cone type gives rise to its own separate visual image (or neuronal representation). When the three images – defined in terms of a pattern of areas with relative lightness – are compared (somewhere at the brain level?), they may be found to be inconsistent with each other. This inconsistency signals "hue". If they to be all three alike, this signals that you are looking at a monochrome picture or scene.
Compare this with the fact that your left and right eye give you two images that are not perfectly alike. This inconsistency between the two images provokes the perception of the quality of "depth".
So in the retinex theory hue is defined as "a relation of relations", very far from the absolute colorimetic value of the local stimulus at a spot in the optical image projected on the retina. This definition of hue makes it invariant under diverse variations in the optical stimulus, for instance due to variations in the quality and intensity of prevaling illumination. In a series of experiments Land and his collaborator John McCann later on followed up this aspect of the retinex theory. (How a specific quality of hue follows from the presumed comparison of the three retinexes, is however still not clear to me.)
Immediately after Land had published his two-colour projection experiment his papers were critically evaluated. It was pointed out that all of his observations could be explained by already well-known facts about colour vision. As a sweeping statement this is true, but there are definitely some thought provoking features of his seemingly naive way of approaching this intriguing issue.
It is, for instance, a popular misunderstanding concerning colorimetry that the trichromatic measure (x,y,Y) of a light ray, impinging on the retina, should determine the colour at the corresponding spot in the visual field. What colorimetry predicts is which spectral compositions of light are equivalent as stimulus to the retinal receptors. But how these equivalent lights look is something colorimetry does not tell us. The (x,y,Y)-values can be used to describe the optical image momentarily projected on the retina, but that image is not what we see. We rather see by help of it.
A valuable feature of Land's approach is that he gives images (i.e. stimulus patterns as such) the primary role in vision. Traditionally, point-wise stimulation of the retina by impinging radiation has been assumed to supply the primary elements out of which a so called "visual image" is secondarily composed. This "atomistic" view had been questioned already by the gestalt-psychologists at the beginning of last century. They prefer a field-theoretical approach where certain structural features, "gestalts", such as figure/background, serve as elementary concepts.
For instance, in an ambiguous figure/background picture it can happen that when you see a certain shape as figure it has hue, but when you see it as background it is neutral, i.e. without hue. In that experiment nothing physical, nothing in the stimulus pattern on the retina, has changed.
Land goes an important step further than conventional scientific investigators in that he speaks of the "natural image". Which can be interpreted as meaning: not confined to laboratory situations. In his (initial) experiments you are not constrained to look "in a certain way", with a fixed position of head etc. And the scene should preferably be quite complicated, in terms of the various parts constituting it.
That many phenomena within perception psychology (e.g. perceptual constancies) demand a certain degree of spatial complexity in order to be stable and clearly observable, is a well-known difficulty in designing experiments in perception research.
Within the hermeneutics of colour vision, several ways have been explored in search for a satisfactory understanding.
A common feature of most traditional approaches is that they expect to explain colour vision phenomena in terms of "mechanisms", realised by physiological processes in the eye and brain. The idea being that the stimulation of the receptors in the retina, via a chain of events, in some way "cause" the sensation of this or that colour in the mind. This view was vaguely held by Newton and his contemporaries.
The subjective sensations of light and colour that arise when certain nerves or brain centra are stimulated electrically or mechanically, are taken as support for this kind of theory. Likewise adaptation and contrast give rise to colour phenomena such as afterimages, coloured shadows, simultaneous contrast colours etc. Goethe, in his Farbenlehre, called it "physiological colours" and took them as evidence for the living activity of the sense organ and its capability to produce out of itself what it normally meets from outside .. as he carefully formulated it. (§38)
That physiological adapation and contrast effects, due to interaction between neighbouring areas on the retina, can satisfactorily explain the observations in connection with two-colour projections has been suggested by several commentators. But personally I sympatize with Roger Shepard when he says, after having seen and contemplated one of Land's demonstrations: "... it suggested to me that the principal features of color vision may have arisen as an accomodation to regularities in the world." Which means that one has to look beyond the sensory mechanisms to the world outside. This was the approach of among others James Gibson. He called it "ecological optics".
Gibson's radical approach has many interesting features. He skips the idea of an "inner visual image", as a kind of representation in our mind or brain of the outer world. He stresses that perception is an ongoing process, not a series of snapshots based on the momentary stimulation of the retinal receptor mosaik. This means that the limitations of the capacity of our visual organ (such as for instance the trichromaticity of the retinal receptor mosaik) does not mean any a priori limitation for perception, for instance to discriminate surfaces with different spectral reflectance, namely by studying them in various illuminations.
We also know that eye movements, shifting of direction of gaze as well as rapid micro oscillations, are necessary for colour vision. Even this bears witness to perception as a continuously ongoing activity.
Allmost all investigations of visual functions have been based on images in form of plane pictures or retinal projections. We have expected to understand visual perception on the basis of how we see pictures. Gibson points out that this may have been a fundamental mistake, arising from a fascination of the "camera obscura" model of vision. Actually it ought to be the other way round: we have to try to understand how we see pictures by help of our knowledge about vision i real situations, with objects in space.
And, as Gibson says, it is more difficult to understand how we see pictures, than how we see reality. As in our case, when we look at a plane projection of a picture that can be seen as representing physical objects on a shore, all in reddish illumination. Can what we see in the two-colour projections be explained by reference to a corresponding real situation? That is what I tried in my study above.
The idea, that the sense qualities should be produced by the sense organs might be a fundamental mistake. We do not see the activity of the processes that make vision possible. On the contrary! We see through our eyes, and by help of our eyes, we do not see the eyes! We do not see the inverted image optically projected on the retina. We see by help of it. And we do not see the radiation stimulating the retinal receptors. We see illuminated or luminous object surfaces "out there" by help of the radiation.
The experience of constancy of object surface colours under chromatically varying illumination can be related to an invariant physical property of the surface -- its spectral reflectance (or at least the first order properties of this). This "physicalistic" idea seems attractive, but does not grasp the very essence of colour, I suspect.
Moreover, since we are now speaking of pictures, not real physical objects in space, the information we get about the things represented is limited. It might even, as in our case, be inconsistent or contradictory:
On the one hand, the fact that the green and blue records are exactly the same indicates that it might be a monochrome picture. On the other hand, the existence of certain objects -- e.g. the red boat -- with a hue of high saturation, indicates that we are looking at a scene with coloured objects. The visual system has to settle this problematic contradiction. And it does: when I see the picture as a representation of illuminated coloured objects, then I also see definite hues on the surfaces of these objects. (But another person may very well see other hues, or for instance just grey!)
This ambiguity, due to the duality of the information, and our visual systems capacity to handle it, is the most interesting aspect of the two-colour-projection demonstration.
*
This takes us over to a more strictly phenomenological point of view. When Gibson speaks of "the scene behind the screen" this is how we experience it, for instance at the cinema. But it is not literally true -- there is no scene or picture behind the screen. Nor is what I perceive situated on the screen, or in my brain, but in some sense between me and the screen. This "in-between" must however not be taken in a spatial sense.
Furthermore, we may have to take "qualitative colour" (consciously experienced colour) seriously, as an entity in its own right.
In his article "Sinneswahrnehmung und Naturwissenschaft" the physiologist Herbert Hensel stresses that visual perception is an intentional act. Hence "die Qualitäten sind logisch irreducibel" and belong to "die Kategorie der Inhaltlichkeit". Which means: It is something you cannot explain by studying the means by which it is actualised or manifests itself.
This concerns,among other things, the dichotomy between primary and secondary sense qualities, based on the idea that secondary qualities should be explainable in terms of the primary ones. A possibility denied by Hensel.
The unconventional way of thinking here is that we, on the one hand, are used to consider colour as belonging to "the way we see the world" (we see the world in terms of, or clothed in colour). That is to say as a basic ingredient of vision itself. And now, on the other hand, we must be open to the possibility of regarding colour (also) as something we meet among other things in the world, as it presents itself in and through various colour phenomena.
Hence the "great basic laws of colour vision", Land held that his two-colour projections revealed, perhaps cannot ever be formulated as such (i.e. the way physical laws of nature are formulated). But we can approach them with reference to "general principles". Such as when Goethe says, in his Farbenlehre: Colour strives to present itself as a totality. The whole gamut of colours will always tend to appear (§60).
For instance, as long as we do not establish conditions that prevent blue from appearing, it will show up.
Edwin Land: "Color Vision and the Natural Image", Proc. Natl. Acad.Sci. 45 (1) Jan 1959
Edwin Land: "Experiments in Color Vision", Scientific American, May 1959
Edwin Land: "The Retinex", American Scientist 52 (2) June 1964
Edwin Land: "Recent advances in retinex theory", in ed. Byrne and Hilbert: Readings on Color, Volume 2, p.143-159 (1997)
Roger N. Shepard: "The perceptual organization of colors: An adaptation to irregularities of the terrestrial world?" in Byrne & Hilbert, as above, especially page 318-321.
N Ribe and F Steinle: "Exploratory Experimentation. Goethe, Land, and Color Theory", Physics Today, July 2002
Michael H. Wilson: What is Colour? The Collected Works. Phänomenologie in der Naturwissenschaft, Band 12. Logos Verlag Berlin 2018.
James J. Gibson: "The Ecological Approach to Visual Perception" 1979. Therein especially chapter 15, "Pictures and Visual Awareness".
Herbert Hensel: "Sinneswahrnehmung und Naturwissenschaft", Studium Generale, Jahrg.15, Heft 12, p.747-757, 1962.
Herbert Hensel:"Die Sinneswahrnehmung des Menschen", Musiktherapeutische Umshau 1, 203-218 (1980)
(C) Pehr Sällström, 2019-08-17