Footnotes to the Film
The idea
behind the film was not to present already established facts and theories in a
popular form. It rather presents as series of demonstrations that raise
questions which force us to start thinking.
In
physics, observation goes hand-in-hand with imagination. How can we avoid
getting snared by the magic of the appealing demonstrations of classical optics?
What are the underlying postulates that were never explicitly formulated?
What does it mean to understand the world through mathematical concepts?
For instance, to understand the nature of Light in terms of "Rays"?
I think
a good film should illuminate a number of questions without trying to answer
them.
However, should you like to get a somewhat more
elaborated commentary to what is shown in the film than the very concise
statements that accompany
the visual aspect of it – here
follows some supplementary notes.
You
are invited to contribute to the notes! Send a mail to pehr@pscolour.eu
and I will put your comment into this page.
PRELUDE
An
important aspect of the kind of investigation here documented is the careful
attention to each phenomenon as a whole. Trying to keep all relevant aspects in
sight. We may call it a holistic approach. I
start my exposition with the statement that each image has its counter image.
This idea is intuitively self-evident as long as we are concerned with
simple pictures in black and white. Just interchange the black and white areas!
It was the ingenious idea of Goethe to study such complementary designs in black
and white through a prism, thus establishing a rule of pairwise correspondence
between colours, directly following from the symmetries of the geometrical
conditions. He saw therein a ground for the notion of
"complementary colours", since long figuring in discourses on
the art of painting.
His own
interpretation of the phenomenon was that colour always presents itself as a
totality. The given instance before ones eyes implicates its opponent colour,
which is potentially present and
ready to appear "the moment a suggesting cause presents itself", as
Goethe says in §69 of his "Farbenlehre", where he discusses the
phenomenon of coloured shadows.
Complementarity
The complementarity between the two types of spectra is clarified in the
diagram below.
 |
Suppose
you make a small hole in a plate and use it to produce a Newtonspectrum,
by placing it in a flux of dispersed light. The small disk that you had
to cut out to make the hole, if put into the light flux, casts a shadow
in the shape of a
Goethespectrum. Of course, if you try to produce the two spectra
simultaneously at one and the same place by putting back the small disk,
the result will be total darkness. Thus we may properly call the two
kinds of spectra
complementary, in so far as the conditions for there existence are
complementary. Furthermore,
if the plate is a mirror, on the reflecting side you will get a
Goethespectrum and the small disk will reflect a Newtonspectrum. Again,
if we put the reflecting objects together, the two spectra will inhibit
each other, in this case with plain white as a result.
|
Furthermore,
complementarity is not just a question of adding two coloured light fluxes
together, by superimposing them, and getting white light as a result. Nor is it
a question of putting two transparencies on top of each other and getting
opacity as a result. No, the
complementarity we get to know here is more fundamental. It holds between
aspects of one and the same entity. Aspects, or moments, that by necessity
belong to each other, as do the two sides of one and the same paper. This is
what we call "the formal ontology of light and colour".
In any
theory formal ontological clarifications are necessarily prior to the empirical
investigation. This is what Goethe alludes at, when saying: "to know that
heaven is everywhere blue, you don’t have to travel the world around".
It is also therefore he is entitled to say, in his conversation with
Eckermann, on the 18:th of March 1831: "…meine Farbenlehre is so alt wie
die Welt."
It seems to me that, in
general, Goethes experimental procedure aims at clairfying necessary relations
that hold between aspects of one and the same whole, aspects that we are used to
describe as being independently
existing. And therefore tend to treat
as if they were independently existing.
EXPERIMENTAL SET-UP
If light does not
illuminate some object it is invisible. So the flow of light and the colour
phenomena produced in it need to be visualized. One way of doing this is by help
of fine dust or mist. Another often used and more convenient method is to
project the light flow onto a sloping white board. The rays we see on the board
are not coincident with the light rays themselves, but it is in our case a fair
representation of these. Because of
the way a prism acts, due to its shape, the geometrical optical phenomena we are
going to study are essentially two-dimensional, which permits this simple way of
simultaneously visualizing the various stages of the metamorfosis of the colour
spectra along the light way.
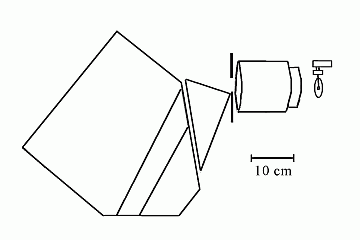 |

Height of prism:
85 mm
Width of light path:
55 mm
Slit in mirror:
1 mm
|
Note, that a "ray" is a concept, not an observable
physical entity. The only observable involved is the event of
absorption of a photon. And the place where it happens is the endpoint of a
ray. An experimental observation involves a statistics of such absorption events
at a certain place and time. Then you repeat the observation after moving the
detector to another place, assuming a stationary state of the flux of light, so
that it does not matter that this observation is done at a later time. It
turns out that the material, cleverly analysed and ordered, can suitably be
described as the flux of light following straight lines in space, the so called
rays. Next step is to visualize this concept in a proper way. (In my film I
produce a kind of "meta-rays", being constituted by a series of
end-points of rays.)
"Dispersed light"
One thing that especially
caught my imagination when reading Holtsmarks article was the idea of a space
illuminated by seemingly ordinary white light, but having the pecular inner
quality of being "dispersed" after having passed the border between
two media of different optical density. Not
until you start experimenting with various objects in that light its secrets are
revealed. That was the reason why I wanted a prism as big as possible and it was
also the reason why I choose to fade out the boundary colours of my "light
road".
As a
matter of fact "white light" is far from a simple concept. The quality
of daylight varies appreciably, depending on the time of the day, weather
conditions etc., and we humans have invented various kinds of artificial light
sources – all giving an illumination that falling onto a white paper looks
colourless, neutral, i.e. just "white". As
soon as colour samples are introduced into the illuminated field they may look
shockingly different from their ordinary look, revealing the qualitative
peculiarity of the light. I had earlier studied effects of this kind (so called
"metamerism") quite extensively, in connection with an evaluation of
the colour rendering properties of artificial light sources. So I knew that this
way of demonstrating the relationship between light and colour is both
spectacular and thought provocative.
PLAYING WITH A MIRROR
As you know, left and right are interchanged when
you look into a mirror. So the reflected image, with a blue boundary spectrum,
in the figure below, actually corresponds to the spectrum that would
appear at the left side of the original light-path. (Whereas the
yellow-red boundary spectrum appears at the right side, as you
see.) When you see this demonstrated in the film, the first time, it could
be a bit confusing.

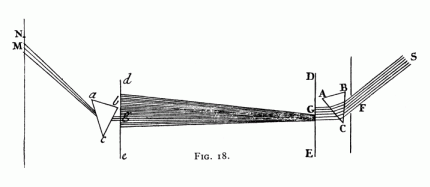
DECOMPOSING THE SPECTRUM
The diagram shown in the
film is taken from Propr. II, Theor. II, Exper. 6,
Fig. 18,
in Optics (1704) and the quotation is from Book One, Part I.
Newton
further says:
All homogeneal Light
has its proper Colour answering to its degree of Refractibility, and that Colour
cannot be changed by Reflexions and Refractions. Opticks,
Book One, Part II. (PROP. II THEOR. II)
Concerning the concept of "Rays"
The ray concept itself is old – rays are seen already on old
egyptian paintings and reliefs. How did humans come to think about light as
rays? Because there is also darkness. The idea of the rectilinear propagation of
light wouldn’t have appeard if there had not been objects casting shadows,
linearly drawn by the sun on the ground or floor.
Rays signify the experience of direction, of light arriving as
illumination from a certain direction – the direction of the sun or any other
localized light-source.
On the other hand, in an illuminated space light is just present. It is a
state of the space, in the same way as total darkness is a possible state of the
space. So what gives us the right to speak of light as fragmented into rays?
Most textbooks in optics either avoid defining the concept of
"light-rays" or else name it as "the path along which light
travels" or "path of shortest optical length". The concept is
however more thoroughly discussed by the mathematician Georg Unger, in his book "Von
Bilden Physikalische Begriffe", Teil II (1961), and similar ideas are found
in the writings of the American perception psychologist James Gibson.
Georg
Unger:
Ohne materielle (genauer: undurchsichtige) Körper kann die
Geradlinigkeit der Lichtausbreitung nicht festgestellt werden. (13)
Wenn immer wir Lichtstrahlen Zeichnen, sind wir uns
bewusst, dass ihre Berechtigung darin besteht, dass sie durch geeignete Blenden
als Licht-Schatten-Grenzen verwirklicht werden können. Die Lichtstrahlen sind mögliche
Licht-Schatten oder Bedeckungsgrenzen. (14)
Die geometrischen Konstruktionen und phoronomischen Bilder, die mit der
Ausbreitung des Lichts verknüpft werden, beziehen sich grundsätzlich auf
Erscheinungsort und Verschwindungsstelle unter berücksichtigung, praktisch der
am Lichtwege liegenden, theoretisch aber aller im Raum befindlichen, materiellen
Körper. (15)
James
Gibson: Ecological
Optics (1960): In ecological optics a ray should not be conceived as a beam of light, not even
as one which vanishes to a geometrical line, but as a transition between one
beam, and the next. It is the locus of change
in light energy over the array.
The concept of a beam of light which becomes vanishingly thin but still retains
a given intensity and spectral character is troublesome. Such a fiction may be
useful for geometrical optics, and convenient for the tracing of rays through
refracting media, but it cannot stimulate an eye. A transition, however, can
stimulate an eye. The rays of ecological optics, being the loci of transitions,
are not infinitely dense as they are supposed to be in pure geometry. Ecological
optics does not have to be concerned with the problem of waves or particles, nor
with the laws of refraction, reflection, and diffraction. It is primarily
concerned with margins, borders, contrasts, ratios, differences and textures in
the optic array. (258)
Now listen to how Isaak Newton
in his time
defined Rays, in his famous book Opticks:
By
the Rays of Light I understand its least Parts, and those as well Successive in
the same Lines, as Contemporary in several lines (...) The least Light or
Part of Light, which may be stopped alone without the rest of the Light, or
propagated alone, or do or suffer any thing alone, which the rest of the Light
doth not or suffers not, I call a Ray of Light.
Note 1:
Newton
does not speak of the Light
of the Sun, but of the Rays of the Sun. This is in plural!
Note 2: Newton's view was not totally unlike
the way many a physicist of today still looks upon light. Namely as a flux of an
enormous number of quasi-particles, the photons, each photon being solitary and
totally "unaware" of the others.
But
an important difference is this: there are no different kinds of photons. The photon is one
elementary particle among others, perculiar by being massless and having spin
one. The frequency (and wavelength) is not a property of the photon. It depends on the quantum of energy that it
happens to transmit -- and that is statistically determined by the particular
material configuration, including the light source. And that energy influences
how the photon behaves on its way between the point of emission and that of
absorption. Furthermore: the photon is not a "Ray", nor a
point-wise localized particle, nor a wave-motion in some medium or field.
It is rather a coincidence between two events in space-time: the emission and
the absorption of a quantum of energy.
In fact these modern rays, the photons, have a very solitary existence.
They do not know of each other, just being momentary coincidences of emission-
and absorption-events in an eternity of time and infinity of space. Light fluxes
that are superimposed just add without any interaction. A light beam does not
"take up space", does not (like matter) make itself impenetrable.
HOLTSMARK´S IDEA
The
important feature of Holtsmark's approach in the paper from 1960 is the
consequent use of mirrors instead of absorbing plates to delimit and diverge the light
flux. With mirrors no light is
eliminated – the light flux is split in two parts, which can both be followed
and studied on equal footing with each other. This
helps us see clearly how the material conditions by necessity give rise to
complementarity in the optical phenomena.
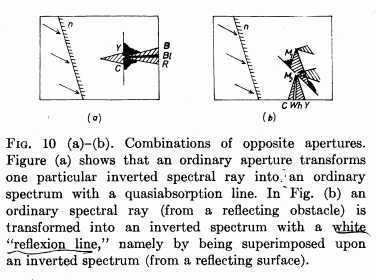
Two crucial diagrams from Torger Holtsmark's article
from 1970.
Figur 11 describes the arrangement implemented in
the film. Figur 10 describes an alternative arrangement, in which you can see
how a dark absorptionline in an ordinary spectrum corresponds to a white line in
the invertred spectrum. In our set-up with parallel slit-mirrors the two cases
in principle look like this:
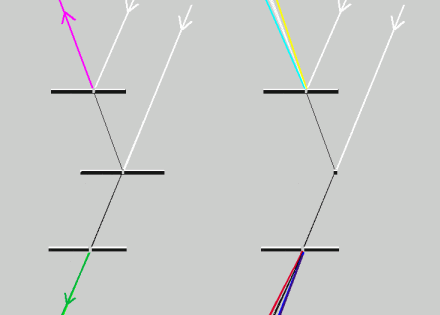
TWO REFLECTING
APERTURES
Explanation in terms of supersposition of
complementary spectra.
How
do you explain the purple ray? What
kind of illusion is this? Is it not typical
for illusionists to make trick with mirrors!
The picture below can perhaps help
you understand what goes on.
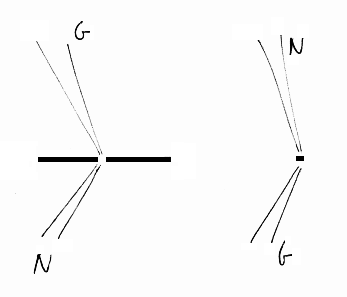
|

|
| Turkois ray coming from below. Seems to continue on the
upper side. |
Nothing comes from below. G-spektrum on the upper side. |
White light from below. Totally white field on the upper
side. |
What propagates through
the hole is not a purple ray. But a dark ray that however gets illuminated on
the other side, thus turning into a purple ray! It
gets its colour by being an illuminated shadow. Darkness cannot bring its colour
with it …
The
phenomenon of "coloured shadows"
(shadows that are not just black och grey, due to the interplay between at least
two light sources of different spectral quality) is important to the
understanding of human colour perception and Goethe played a lot of attention to
it, in his old days discussing with Eckermann how it might be explained. In many
practical situations the phenomenon is not ideally realized (the shadow does not
appear on a perfectly white field) due to circumstances, and the visual process
then tends to change the visual image in the direction of the ideal case,
through chromatic adaptation. Because of this it has usually (as by Goethe) been
designated as a physiological colour, or subjective colour. But in the present
case it is as objective (or subjective, if you prefer) as the green colour of
the monochromatic light ray on the dark side of our apparatus.
How to explain the phenomenon along the
lines of Newton's ideas
You can
explain the purple line with help of the newtonian concept of rays
of light that superimpose. To simplify: Think of the light falling towards the
arrangement of mirrors as being constituted by the superimposed light fluxes
from three lamps: a red, a green and a blue,
mounted a little beside each other, thus shining from slightly different
directions. And apply the well-known rule that the light fluxes pairwise add to cyan,
magenta, yellow and all three together add up to white.
First
put on only the green light. With
suitably
arranged mirrors you get a green ray on the dark side and a black ray in green
environment, on the bright side of the mirrors.
Then put
on the red and the blue lamp. The black ray turns into a purple ray, since it is
illuminated from the sides by red and blue light, adding up to purple.
So the purple ray is a kind of coloured shadow!
Look
upon this display from increasing distance and you will see how the image of a
purple line on grey background emerges.

Note. The purple
ray in the light field could be used as a signal. It could be interpreted as
information about something being the case, in connection with that specific
direction. The direction of propagation of information is however
not the same as the direction of propagation of energy in the field, as it would
be in the ordinary case, when light rays are used to mediate the
transmission.
WHAT DO WE LEARN FROM THIS?
Besides that I present
Goethe's idea of the principle of complementarity as central in colour
theory, and that I show how the use of mirrors is essential, when you want
to demonstrate the principle, my study mainly concerns the concept of "Rays
of Light". My conclusion is that Rays (even when you suggestively see them
before your eyes and photograph them) are just constructs, artefacts,
"Gebilde", in the medium of light. But never light itself! It
remains enigmatic.
CONCLUSION
The case of "comb filtering", i.e. when
neighbouring N- and G-spectra are made to overlap more and more, ending up in
just grey, is shown in the clip below.
PSColour/fotnoter_uk.htm 2010-05-03 revised 2010-09-16